快速幂

写成函数：

long long PowerMod(long long a,long long b,long long c)
{
    long long ans=1;
    long long k;
    k=a;
    k=k%c;
    while(b>0)
    {
        if(b&1)
        ans=(ans*k)%c;
        b>>=1;
        k=(k*k)%c;
    }
    return ans;
}

矩阵快速幂

以求斐波那契数列第n(1 <= n <= 10^18)项为例，由于结果很大，输出F(n) % 1000000009的结果即可。

因为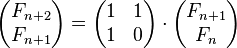

所以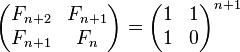

求Fib(n) % P的问题转为了求矩阵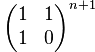

矩阵快速幂的写法跟快速取幂法相似：

#define MOD 1000000007
struct mat
{
    long long a[2][2];
}m,r;
mat mult(mat x,mat y)
{
    mat res={0};
    int i,j,k;
    for(i=0;i<2;i++)
    for(j=0;j<2;j++)
    for(k=0;k<2;k++)
        res.a[i][j]=(res.a[i][j]+(x.a[i][k]*y.a[k][j])%MOD)%MOD;
    return res;
}
mat PowerMod(mat x,long long n)
{
    mat ans={0};
    int i,j;
    for(i=0;i<2;i++)
    ans.a[i][i]=1;
    while(n>0)
    {
        if(n%2==1)    
        ans=mult(ans,x);
        x=mult(x,x);
        n=n/2;    
    }
    return ans;
}
int main()
{
    long long n;
    scanf("%lld",&n);
    m.a[0][0]=1;m.a[0][1]=1;m.a[1][0]=1;m.a[1][1]=0;
    r=PowerMod(m,n-2);
    printf("%lld\n",r.a[0][0]);
    return 0;
}