强连通分量tarjan:https://www.byvoid.com/zhs/blog/scc-tarjan
http://www.cnblogs.com/zufezzt/p/4699731.html
缩点:https://segmentfault.com/a/1190000009187840
求割点:http://www.cnblogs.com/en-heng/p/4002658.html
求桥:http://blog.csdn.net/fuyukai/article/details/51039788
双连通分量:http://blog.csdn.net/fuyukai/article/details/51303292
割边:在连通图中,删除了连通图的某条边后,图不再连通。这样的边被称为割边,也叫做桥。
割点:在连通图中,删除了连通图的某个点以及与这个点相连的边后,图不再连通。这样的点被称为割点。
DFS搜索树:用DFS对图进行遍历时,按照遍历次序的不同,我们可以得到一棵DFS搜索树。在上面例子中,得到的搜索树为:
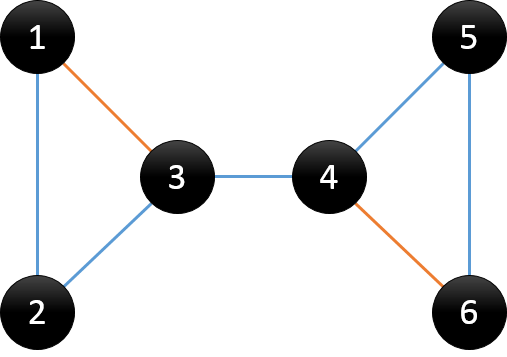
树边:在搜索树中的蓝色线所示,可理解为在DFS过程中访问未访问节点时所经过的边,也称为父子边
回边:在搜索树中的橙色线所示,可理解为在DFS过程中遇到已访问节点时所经过的边,也称为返祖边、后向边
观察DFS搜索树,我们可以发现有两类节点可以成为割点:
- 对根节点u,若其有两棵或两棵以上的子树,则该根结点u为割点;
- 对非叶子节点u(非根节点),若其中的某棵子树的节点均没有指向u的祖先节点的回边,说明删除u之后,根结点与该棵子树的节点不再连通;则节点u为割点。
对于根结点,显然很好处理;但是对于非叶子节点,怎么去判断有没有回边是一个值得深思的问题。
我们用dfn[u]记录节点u在DFS过程中被遍历到的次序号,low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小),那么low[u]的计算过程如下:
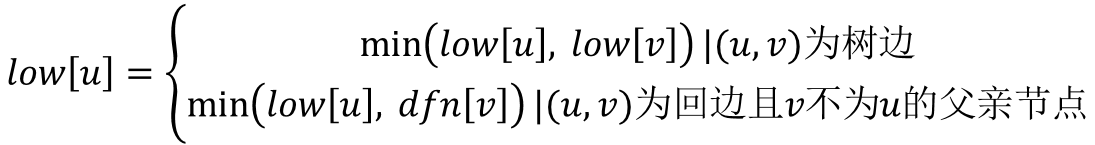
对于给的例子,其求出的dfn和low数组为:
id 1 2 3 4 5 6
dfn 1 2 3 4 5 6
low 1 1 1 4 4 4
可以发现,对于情况2,当(u,v)为树边且low[v]≥dfn[u]时,节点u才为割点。
而当(u,v)为树边且low[v]>dfn[u]时,表示v节点只能通过该边(u,v)与u连通,那么(u,v)即为割边。
若一个无向图中的去掉任意一个节点(一条边)都不会改变此图的连通性,即不存在割点(桥),则称作点(边)双连通图。
对于一个无向图,当我们把图中所有的桥都去掉以后,剩下的每一个区域就是我们要求的边的双连通分量。
POJ 2186
题意:每一头牛的愿望就是变成一头最受欢迎的牛。现在有N头牛,给你M对整数(A,B),表示牛A认为牛B受欢迎。 这种关系是具有传递性的,如果A认为B受欢迎,B认为C受欢迎,那么牛A也认为牛C受欢迎。你的任务是求出有多少头牛被所有的牛认为是受欢迎的。
解题思路: 先用tarjan求出每个强连通分量,再缩点,统计每个点的出度,如果有且只有1个出度为0的点,就输出这个点包含的节点数,否则输出0(如果其点有出度,那么这个点首先一定就不是被所有牛崇拜的对象,所以如果一个点没有出度,那么这头牛就很有可能被所有牛所崇拜。如果出度为0的牛大于两个,那么就说明被所有牛都崇拜的个数为0,因为这里有两头及以上牛互相没有崇拜关系)。
AC代码:
vector<int>v[10010];
vector<int>scc[10010];
int dfn[10010];//在DFS中该节点被搜索的次序
int low[10010];//i或i的子树能够通过非树边追溯到最早的祖先节点(即DFS次序号最小)
int sccn[10010];//缩点数组,表示某个点对应的强连通分量编号
int ot[10010];//每个强连通分量的出度
bool vis[10010];//是否在栈中
int step;
int cnt;//强连通分量编号
stack<int>s;
void tarjan(int u)
{
dfn[u]=low[u]=++step;
vis[u]=true;
s.push(u);
for(int i=0;i<v[u].size();i++)
{
int temp=v[u][i];
if(!dfn[temp])//没有被访问过
{
tarjan(temp);
low[u]=min(low[u],low[temp]);
}
else if(vis[temp])//在栈中
low[u]=min(low[u],dfn[temp]);
}
if(low[u]==dfn[u])//构成强连通分量
{
cnt++;
while(1)
{
int temp=s.top();
s.pop();//此点以上的点全部出栈,构成一个强连通分量
vis[temp]=false;
sccn[temp]=cnt;//cnt是强连通分量的序号
scc[cnt].push_back(temp);
if(temp==u)break;
}
}
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
v[i].clear();
scc[i].clear();
}
while(m--)
{
int from,to;
scanf("%d%d",&from,&to);
v[from].push_back(to);
}
step=cnt=0;
memset(dfn,0,sizeof(dfn));
memset(sccn,0,sizeof(sccn));
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i);
memset(ot,0,sizeof(ot));
for(int i=1;i<=n;i++)
for(int j=0;j<v[i].size();j++)
{
int temp=v[i][j];
if(sccn[i]!=sccn[temp])//如果i点与他指向的点不在同一个强连通分量中
ot[sccn[i]]++;//i点所在的强连通分量的出度+1
}
int pos=-1;
int num=0;//出度为0的强连通分量个数
for(int i=1;i<=cnt;i++)
if(ot[i]==0)
{
num++;
pos=i;
}
if(num==1)printf("%d\n",scc[pos].size());
else printf("0\n");
return 0;
}HDU 2767
题意:至少增加几条边,才能让图强连通。
解题思路:我们要将这个图变成强连通分量为1的图,我们不妨这样考虑:既然强连通分量为1的图有这样的特点:如果一个图是强连通分量为1的图,对于每个节点来说,一定没有任何一个点的出度或者入度有0的情况。那么我们的任务也就明确了,对于所有节点度的处理,使得没有0度的存在。这里设出度为0的节点数为a,设入度为0的节点数为b,其实我们如果找到了a和b的值,搞定最大值,其实也就搞定了这个问题(注意本来就是连通图的情况要特判)。
POJ 1236
题意:
有N个学校,从每个学校都能从一个单向网络到另外一个学校,两个问题1:初始至少需要向多少个学校发放软件,使得网络内所有的学校最终都能得到软件。2:至少需要添加几条边,使任意向一个学校发放软件后,经过若干次传送,网络内所有的学校最终都能得到软件。
解题思路:
在有向无环图中,边变为了强连通分量之间的文件传输关系。意味着:只要一个强连通分量有入边,那么就可以通过这个入边从另外一个分量中接收文件。但是,无环图意味着肯定存在没有入度(入度为0)的强连通分量,这些强连通分量没有文件来源,所以要作为投放文件的位置。那么,第一问就只需要计算出缩点后入度为0的强连通分量数目即可。第二问同HDU2767。
UVA 315
题意:求割点。
解题思路:
在无向连通图G中,
1、根结点u为割顶当且仅当它有两个或者多个子结点;
2、非根结点u为割顶当且仅当u存在结点v,使得v极其所有后代都没有反向边可以连回u的祖先(u不算)
在Tarjan算法里面,有两个时间戳非常重要,一个是dfn,意为深度优先数,即代表访问顺序;一个是low,意为通过反向边能到达的最小dfn。于是,上述定理中第二个条件(非根结点)可以简单地写成low[v]>=dfn[u]。
可作模板。
求割点模板:
vector<int>v[10010];
int dfn[10010];//在DFS中该节点被搜索的次序
int low[10010];//i或i的子树能够追溯到的最早的栈中节点的次序号
bool cut[10010];//是否为割点
int step;
void tarjan(int u,int fa)
{
dfn[u]=low[u]=++step;
int child=0;//孩子结点的数目
for(int i=0;i<v[u].size();i++)
{
int temp=v[u][i];
if(temp==fa)continue;
if(!dfn[temp])//没有被访问过
{
child++;
tarjan(temp,u);
low[u]=min(low[u],low[temp]);
if(u!=fa&&low[temp]>=dfn[u])//当前结点不是根结点
cut[u]=true;
}
else low[u]=min(low[u],dfn[temp]);
}
if(u==fa&&child>1)//当前结点是根结点
cut[u]=true;
}
int main()
{
int n,m,from,to;
char ch;
while(1)
{
scanf("%d",&n);
if(n==0)break;
for(int i=1;i<=n;i++)
v[i].clear();
while(1)
{
scanf("%d",&from);
if(from==0)break;
while(1)
{
scanf("%d%c",&to,&ch);
v[from].push_back(to);
v[to].push_back(from);
if(ch=='\n')break;
}
}
step=0;
memset(dfn,0,sizeof(dfn));
fill(cut+1,cut+n+1,false);
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i,i);
int num=0;
for(int i=1;i<=n;i++)
if(cut[i])num++;
printf("%d\n",num);
}
return 0;
}UVA 796
题意:求桥。
解题思路:可作模板。
求割边模板:
vector<int>v[10010];
int dfn[10010];//在DFS中该节点被搜索的次序
int low[10010];//i或i的子树能够追溯到的最早的栈中节点的次序号
struct a
{
int ansx,ansy;
}ans[10010];
int step,cnt;
bool cmp(a x,a y)
{
if(x.ansx!=y.ansx)return x.ansx<y.ansx;
return x.ansy<y.ansy;
}
void tarjan(int u,int fa)
{
dfn[u]=low[u]=++step;
for(int i=0;i<v[u].size();i++)
{
int temp=v[u][i];
if(!dfn[temp])//没有被访问过
{
tarjan(temp,u);
low[u]=min(low[u],low[temp]);
if(low[temp]>dfn[u])//一条无向边(u,v)是桥,当且仅当(u,v)为树枝边,且满足DFS(u)<Low(v)。
{
int a=u,b=temp;
if(a>b)swap(a,b);
ans[cnt].ansx=a;
ans[cnt++].ansy=b;
}
}
else if(dfn[temp]<dfn[u]&&temp!=fa)
low[u]=min(low[u],dfn[temp]);
}
}
int main()
{
int n,m,from,to,num;
while(scanf("%d",&n)!=EOF)
{
for(int i=0;i<n;i++)
v[i].clear();
for(int i=0;i<n;i++)
{
scanf("%d (%d)",&from,&num);
while(num--)
{
scanf("%d",&to);
v[from].push_back(to);
}
}
step=cnt=0;
memset(dfn,0,sizeof(dfn));
for(int i=0;i<n;i++)
if(!dfn[i])
tarjan(i,i);
sort(ans,ans+cnt,cmp);
printf("%d critical links\n",cnt);
for(int i=0;i<cnt;i++)
printf("%d - %d\n",ans[i].ansx,ans[i].ansy);
printf("\n");
}
return 0;
}POJ 3177
题意:最少加多少条边使图变得双连通(有重边)。
解题思路:
http://blog.csdn.net/lyy289065406/article/details/6762370
http://blog.csdn.net/lyy289065406/article/details/6762432
首先要找出图G的所有【边双连通分量】。
Tarjan算法用来寻找图G的所有【边双连通分量】是最简单有效的方法,因为Tarjan算法在DFS过程中会对图G所有的结点都生成一个Low值,而由于题目已表明任意两个结点之间不会出现重边,因此Low值相同的两个结点必定在同一个【边双连通分量】中! (如果是有重边的话,那么不同的low值是可能是属于同一个边双连通分量的,这个时候就要通过其他方法去求解边双连通分量。)无向图的边双连通分量似乎和求强连通相似…其实也是有原因的…
那么如何解决重边的问题?
1、 构造图G时把重边也考虑进来,然后在划分边双连通分量时先把桥删去,再划分,其中桥的一端的割点归入当前正在划分的边双连通分量。这个处理比较麻烦;
2、 在输入图G的边时,若出现重边,则不把重边放入图G,然后在划分边双连通分量时依然用Low划分。
把每一个【边双连通分量】都看做一个点(即【缩点】)
问题再次被转化为“至少在缩点树上增加多少条树边,使得这棵树变为一个双连通图”。
首先知道一条等式:
若要使得任意一棵树,在增加若干条边后,变成一个双连通图,那么
至少增加的边数 =( 这棵树总度数为1的结点数 + 1 )/ 2
那么我们只需求缩点树中总度数为1的结点数(即叶子数)有多少就可以了。换而言之,我们只需求出所有缩点的度数,然后判断度数为1的缩点有几个,问题就解决了。
求出所有缩点的度数的方法
两两枚举图G的直接连通的点,只要这两个点不在同一个【缩点】中,那么它们各自所在的【缩点】的度数都+1。注意由于图G时无向图,这样做会使得所有【缩点】的度数都是真实度数的2倍,必须除2后再判断叶子。
HDU 4612
题意:有重边的无向图,问添加一条边最多能够减少多少个桥。
解题思路:
这条边肯定是连最远的,边双连通分量缩点重建树,然后dfs找树的直径, 答案就是缩点之后的边数-直径。
重边的处理:用一个k标记,假如这个点到父亲的路有两条,那么第一条可以不走,但是第二条必须要走,因为是重边,这样我的儿子节点也就可以更新low了。
树的直径(最长路)的求法:假设 s-t这条路径为树的直径,或者称为树上的最长路,从任意一点u出发搜到的最远的点一定是s、t中的一点,然后在从这个最远点开始搜,就可以搜到另一个最长路的端点,即用两遍广搜就可以找出树的最长路。
HDU 4635
题意:给你一个有向图,问在保证这个图无重边,无自环,且不是强连通图的情况下,最多可以添加多少条有向边。
解题思路:
找出强联通块,计算每个连通块内的点数。将点数最少的那个连通块单独拿出来,其余的连通块合并成一个连通分量。假设第一个连通块的 点数是 x 第二个连通块的点数是 y, 已经有的边数是 m,
如果使X图强连通,边数最多为x(x-1)(即X图的每个顶点到X图其它每个顶点都有一条单向边);如果使Y图强连通,边数最多为y(y-1);X图和Y图之间只有单项的边,则边数最多为x*y(即X图的每个顶点到Y图每个顶点都有一条单向边)。
通过以上可以求得边数F(DAG)=xy+x(x-1)+y(y-1)=nn-n-xy.即DAG图的边数最多为nn-n-x*y-m。
由于n一定,所以本题就可以转化为求x*y的最小值,又因为x+y=n,可知x一定要和y相差最大,所以x要最小。而且要找的X图一定是入度为0或者出度为0的强连通分量,因为无法删边,如果入度和出度都不为0的话 ,说明该边是一定存在的,就无法用这个式子了。
HDU 4738
题意:给一个无向图,求找出一条边,使得删除这条边以后整个图就不连通了,找出满足的边里权值最小的那个,找不到输出-1。
解题思路:注意细节即可。考虑图本来就连通和不连通的情况,以及最小的权值为0的时候也要有人去背。
POJ 3694
题意:
解题思路:首先运行一次tarjan,求出桥和缩点,那么远无向图将缩点为一棵树,树边正好是原来的桥。每次连接两点,看看这两点是不是在同一个缩点内,如果是,那么缩点后的树没任何变化,如果两点属于不同的缩点,那么连接起来,然后找这两个缩点的LCA,因为从点u到LCA再到点v再到点u,将形成环,里面的树边都会变成不是桥。
2018年全国多校算法寒假训练营练习比赛(第四场)D
题意:给出一个n*m个格子的地图,每个格子都有黄金。小明可以将他所在的格子的黄金收归囊中,并且还可以向下或者向右移动’.’,然后继续收集黄金。小明不能移动到有障碍物‘#’的格子上。小明可以随意地在地图上放置可以传送到地图上某一个确定的格子的传送门。至少要使用多少个传送门才能让他在游戏时无论出现在哪个格子,他都能拿到地图上的所有金子。
思路:首先考虑题目里说要拿到所有金子,意思就是要让整张图强连通,而传送门就相当于至少增加几条边,才能让图强连通。这里数据比较大0<n,m<=1000,如果缩点会爆内存,所以只用这种思想即建好图找出度为0的数量和入度为0的数量,取最大值,而不用缩点,注意这里还是要特判只有一个’.’点的情况。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!