E. Maximum Subsequence

You are given an array a consisting of n integers, and additionally an integer m. You have to choose some sequence of indices b1, b2, …, bk (1 ≤ b1 < b2 < … < bk ≤ n) in such a way that the value of 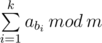is maximized. Chosen sequence can be empty.

Print the maximum possible value of .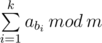

Input

The first line contains two integers n and m (1 ≤ n ≤ 35, 1 ≤ m ≤ 109).

The second line contains n integers a1, a2, …, an (1 ≤ ai ≤ 109).

Output

Print the maximum possible value of .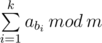

Examples

input

4 4
5 2 4 1

output

3

input

3 20
199 41 299

output

19

Note

In the first example you can choose a sequence b = {1, 2}, so the sum 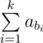is equal to 7 (and that’s 3 after taking it modulo 4).

In the second example you can choose a sequence b = {3}.

题意：给出几个数，每个数字可以取也可以不取，使和的取模最大。

解题思路：这里如果直接搜索的话需要2^35次，所以这里折半搜索，分为前半和后半进行搜索，所以搜2*2^17次就可以了，把前半和后半分别放进set里面，对于前半可以枚举，对于后半就是根据m-1-s[0]来进行二分查找不超过这个值的最大值，然后更新答案即可。

long long a[40];
set<long long>s[2];
long long m;
void dfs(int tp,longlong sum,int l,int r)
{
    if(l==r+1)//这里注意
    {
        s[tp].insert(sum);
        //printf("%d %lld\n",tp,sum);
        return;
    }
    dfs(tp,sum,l+1,r);
    dfs(tp,(sum+a[l])%m,l+1,r);
}
int main()
{
    int n;
    longlong ans;
    scanf("%d%lld",&n,&m);
    for(int i=0;i<n;i++)
    {
        scanf("%lld",&a[i]);
        a[i]=a[i]%m;
    }
    dfs(0,0,0,n/2);
    dfs(1,0,n/2+1,n-1);
    ans=-INF;//注意初值
    set<longlong>::iterator it,it1;
    for(it=s[0].begin();it!=s[0].end();it++)
    {
        longlong x;
        x=m-1-*it;
        it1=s[1].upper_bound(x);
        it1--;//小于等于x的数
        ans=max(ans,*it+*it1);
    }
    printf("%lld\n",ans);
    return 0;
}