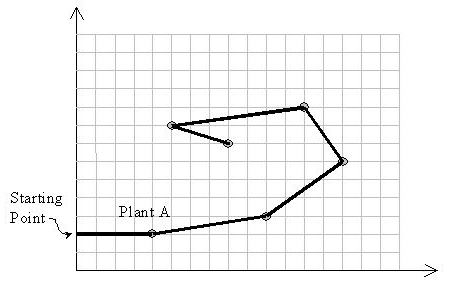
题意：给你平面的一个点集,然后要你从y坐标最小的点开始以水平方向向下一个点连线,每次只能直走或左转,问你最多能走多少点?(输出所有走过的点,且不走回头路,所有点坐标均唯一)

思路：

​ 本题其实就是用极角排序,每次都有一个你的当前点,然后每次都贪心的走以当前点为中心的极角最小的那个点(如果有多个,就走距离当前点最近的那个点即可.)

​ 这样,我们能保证能走过的点数是最多的.

​ 为什么上述贪心算法是对的呢?其实这就是每次都在找最外层的凸包.

完整代码：

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<math.h>
#include<time.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
#include<algorithm>
using namespace std;
struct point
{
    int id;
    double x,y;
}a[110],p[110];
int n,top;
int cur;//记录新的极点
double cross(point p0,point p1,point p2)//叉乘判断在左边还是右边
{
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
double dis(point a,point b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
bool cmp(point p1,point p2)
{
    double c=cross(p[cur],p1,p2);
    if(c>0||(c==0&&dis(p[cur],p1)<dis(p[cur],p2)))
        return 1;
    return 0;
}
void graham()
{
    int pos=0;//最下最左的点
    for(int i=0;i<n;i++)
        if((a[i].y<a[pos].y)||(a[i].y==a[pos].y&&a[i].x<a[pos].x))
            pos=i;
    swap(a[pos],a[0]);
    p[0]=a[0];cur=0;
    for(int i=1;i<n;i++)
    {
        sort(a+i,a+n,cmp);//极角排序
        //printf("(%d)",cur);
        /*for(int j=i;j<n;j++)
            printf("%d ",a[j].id);
        printf("\n");*/
        p[i]=a[i];
        cur=i;
    }
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        for(int i=0;i<n;i++)
            scanf("%d%lf%lf",&a[i].id,&a[i].x,&a[i].y);
        graham();
        printf("%d ",n);
        for(int i=0;i<n-1;i++)
            printf("%d ",p[i].id);
        printf("%d\n",p[n-1].id);
    }
    return 0;
}

在debug的时候找到了一个坐标系上画点的网站：

https://www.desmos.com

挺好用的233333