基本概念

参考博客：http://www.renfei.org/blog/bipartite-matching.html

http://blog.csdn.net/sixdaycoder/article/details/47680831

https://www.cnblogs.com/logosG/p/logos.html

二分图：简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。准确地说：把一个图的顶点划分为两个不相交集 U 和V ，使得每一条边都分别连接U、V中的顶点。如果存在这样的划分，则此图为一个二分图。二分图的一个等价定义是：不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰，我们以后都把它画成图 2 的形式。

匹配：在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。例如，图 3、图 4 中红色的边就是图 2 的匹配。

我们定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点，其他顶点为未匹配点；1-5、4-7为匹配边，其他边为非匹配边。

最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。

完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。

二分图的最大匹配（匈牙利算法）

交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。

增广路： 从一个未匹配点出发，依次遍历未匹配边、匹配边、未匹配边，这样交替下去，如果最后一个点是未匹配点，这条路径称为增广路。换句话说，起点和终点都为未匹配点的交错路为增广路（agumenting path）（特别提醒，这里的增广路和网络流中的增广路的意义不同）。

例如，图 5 中的一条增广路如图 6 所示（图中的匹配点均用红色标出）：

观察图6我们可发现增广路的一些特点。

1. 增广路一定有奇数条边。
2. 增广路中未匹配边一定比匹配边多一条（因为是从未匹配点出发走交错路到未匹配点结束）

这里其实就表明了研究增广路的意义。
如果找到了一条增广路，那么将未匹配点与匹配边的身份调换,那么匹配的边数就多了一条，这样直到找不到增广路为止，那么整个图的匹配的边数一定最大，也就是找到了二分图的最大匹配。

这里的身份调换是指 ：
原来匹配的边为edge(1,6),edge(4,8)，匹配边数为2。找到一条增广路（这里不一定从9开始找，任何一个未匹配点都可以）后，现在匹配的边为edge(2,6),edge(1,8),edge(4,9),匹配边数为3。

匈牙利算法正是利用了增广路的这个性质，从X集合中找到一个未匹配点，寻找增广路，找到了匹配数+1，如果没有找到，那么从X中找到下一个未匹配的点，再次寻找增广路……重复上述过程，直到X集合中的所有节点都被“增广”完毕，无论如何都找不到增广路，那么整个图的匹配数就最大了。

我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的。在给出匈牙利算法 DFS 和 BFS 版本的代码之前，先讲一下匈牙利树。

匈牙利树一般由 BFS 构造（类似于 BFS 树）。从一个未匹配点出发运行 BFS（唯一的限制是，必须走交替路），直到不能再扩展为止。例如，由图 7，可以得到如图 8 的一棵 BFS 树：

这棵树存在一个叶子节点为非匹配点（7 号），但是匈牙利树要求所有叶子节点均为匹配点，因此这不是一棵匈牙利树。如果原图中根本不含 7 号节点，那么从 2 号节点出发就会得到一棵匈牙利树。这种情况如图 9 所示（顺便说一句，图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路，沿这条增广路扩充后将得到一个完美匹配）。

易懂版本参考博客：http://blog.csdn.net/dark_scope/article/details/8880547

代码（增广路注释）：

int n;
vector<int>v[110];
bool vis[110];
int link[110];//右列中与之匹配的左边的
bool judge(int id)
{
    for(int i=0;i<v[id].size();i++)
    {
        int temp=v[id][i];
        if(!vis[temp])//不在交替路中
        {
            vis[temp]=true;//标记在交替路中
            if(link[temp]==-1||judge(link[temp]))//如果是未盖点，说明交替路是增广路，则交换路径，并返回成功
            {
                link[temp]=id;
                //link[id]=temp;//如果左边一列与右边一列编号不同就带上这句
                return true;
            }
        }
    }
    return false;//从id出发没有增广路
}
int maxmatch()
{
    memset(link,-1,sizeof(link));
    int num=0;
    for(int i=1;i<=n;i++)
    {
        memset(vis,0,sizeof(vis));
        if(judge(i))
            num++;
    }
    return num;
}
int main()
{
    int m;
    scanf("%d%d",&n,&m);
    m=m-n;
    for(int i=1;i<=n;i++)
        v[i].clear();
    int x,y;
    while(scanf("%d%d",&x,&y)!=EOF)
    {
        if(x==-1&&y==-1)break;
        v[x].push_back(y);
        //v[y].push_back(x);
    }
    int ans=maxmatch();
    if(ans==0)printf("No Solution!\n");
    else printf("%d\n",ans);
    return 0;
}

代码（易懂注释）：

int n;
vector<int>v[110];
bool vis[110];
int link[110];//右列中与之匹配的左边的
bool judge(int id)
{
    for(int i=0;i<v[id].size();i++)
    {
        int temp=v[id][i];
        if(!vis[temp])//如果可以匹配并且还没有标记过(这里标记的意思是这次查找曾试图改变过这个人的归属问题，但是没有成功，所以就不用瞎费工夫了）
        {
            vis[temp]=true;
            if(link[temp]==-1||judge(link[temp]))//没人匹配或者与之匹配的人可以腾出个位置来，这里使用递归
            {
                link[temp]=id;
                return true;
            }
        }
    }
    return false;
}
int maxmatch()
{
    memset(link,-1,sizeof(link));
    int num=0;
    for(int i=1;i<=n;i++)
    {
        memset(vis,0,sizeof(vis));
        if(judge(i))
            num++;
    }
    return num;
}
int main()
{
    int m;
    scanf("%d%d",&n,&m);
    m=m-n;
    for(int i=1;i<=n;i++)
        v[i].clear();
    int x,y;
    while(scanf("%d%d",&x,&y)!=EOF)
    {
        if(x==-1&&y==-1)break;
        v[x].push_back(y);
        //v[y].push_back(x);
    }
    int ans=maxmatch();
    if(ans==0)printf("No Solution!\n");
    else printf("%d\n",ans);
    return 0;
}

匈牙利算法的要点如下

1. 从左边第 1 个顶点开始，挑选未匹配点进行搜索，寻找增广路。
   1. 如果经过一个未匹配点，说明寻找成功。更新路径信息，匹配边数 +1，停止搜索。
   2. 如果一直没有找到增广路，则不再从这个点开始搜索。事实上，此时搜索后会形成一棵匈牙利树。我们可以永久性地把它从图中删去，而不影响结果。
2. 由于找到增广路之后需要沿着路径更新匹配，所以我们需要一个结构来记录路径上的点。DFS 版本通过函数调用隐式地使用一个栈，而 BFS 版本使用 prev 数组。

补充定义和定理：

最大匹配数：最大匹配的匹配边的数目

最小顶点覆盖：假如选了一个点就相当于覆盖了以它为端点的所有边。最小顶点覆盖就是选择最少的点来覆盖所有的边。很显然，最大匹配中的结点满足该性质，也就是说

最小顶点覆盖数=最大匹配数

最大独立集 ： 二分图中最大的一个点集，该点集内的点互不相连（没有边相连）。回想一下图4 : 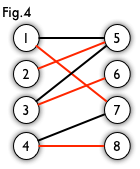显然这里给出了图的一个最大匹配，将最大匹配中的点从原来的节点集合V中删除，那么剩下的点不会有任何边相连，也就是说

最大独立集数目=|V|−最大匹配数

最小路径覆盖数：对于一个 DAG（有向无环图），选取最少条路径，使得每个顶点属于且仅属于一条路径。路径长可以为 0（即单个点）。

最小路径覆盖=最大独立集=|V|−最大匹配

无向图的最大团: 从V个顶点选出k个顶点，使得这k个顶点构成一个完全图，即该子图任意两个顶点都有直接的边。

最大团 = 补图的最大独立集

二分图最大权匹配（KM算法）

参考博客：http://blog.csdn.net/zxn0803/article/details/49999267

https://www.cnblogs.com/wenruo/p/5264235.html

相等子图是原图的一个生成子图（生成子图即包含原图的所有结点，但是不包含所有的边）,并且该生成子图中只包含满足lx(x)+ly(y)=weight(x,y)的边,这样的边我们称之为可行边。

步骤如下：
首先用邻接矩阵存储二分图，注意：如果只想求最大权值匹配而不要求是完备匹配的话，请把各个不相连的边的权值设置为0。
之后进行下述步骤：
1.运用贪心算法初始化标杆。
2.运用匈牙利算法找到完备匹配。
3.如果找不到，则通过修改标杆，增加一些边。
4.重复2，3的步骤，找到完备匹配时可结束。
标杆分为X标杆和Y标杆，一般我们把比较少的点放在X标杆一侧。
这样进行算法：
首先要初始化两个标杆分别为X标杆和Y标杆，X标杆初始化为与之相连的最大边权，Y标杆初始化为0，且直接加入拥有最大边权的边。如果发现此时的匹配就是完备匹配，那么直接退出，否则进行标杆的更改。从第一个节点开始扫描，如果有合法的增广路，那么将其反选，扩充路径，如果该节点没有合法的增广路，那么则将增广路上的所有的X标杆上的点加入点集S,将Y标杆上的所有点加入点集T，从S和不在T集合中的点里面，计算d=min{L(x)+L(y)-w(x,y)};计算后，将在S点集内的x的顶标减d，在T的y的顶标加d。并将目前没有加入二分图的权值和等于顶标和的边作为未匹配边加入到二分图中，然后再在该节点寻找增广路，如果还是没有，则再次通过更改标杆来增加边，直到有增广路出现为止。之后重复寻找增广路的步骤以及更改标杆的步骤，如果出现了完备匹配，那么直接退出。
我认为：求d的过程是把xy的顶标和及其权值相差最小的边加入到二分图中，而修改顶标的过程是使得其顶标之和等于新增入的边权，并使得之前选择的那些边仍然存在（即其顶标和仍等于权值和）。
看得有点绕？
我们来看一下强行手工模拟：
有邻接矩阵如下：
x1 x2 x3 x4 x5
y1 7 3 14 19 23
y2 8 10 15 18 20
y3 6 8 12 16 19
y4 4 9 13 20 25
y5 2 7 12 10 15
非常完美的一个邻接矩阵，其中斜体为边权最大值。下面我们按照上面的晕乎乎的步骤来进行模拟吧。

初始化标杆使X标杆的值为斜体字的值。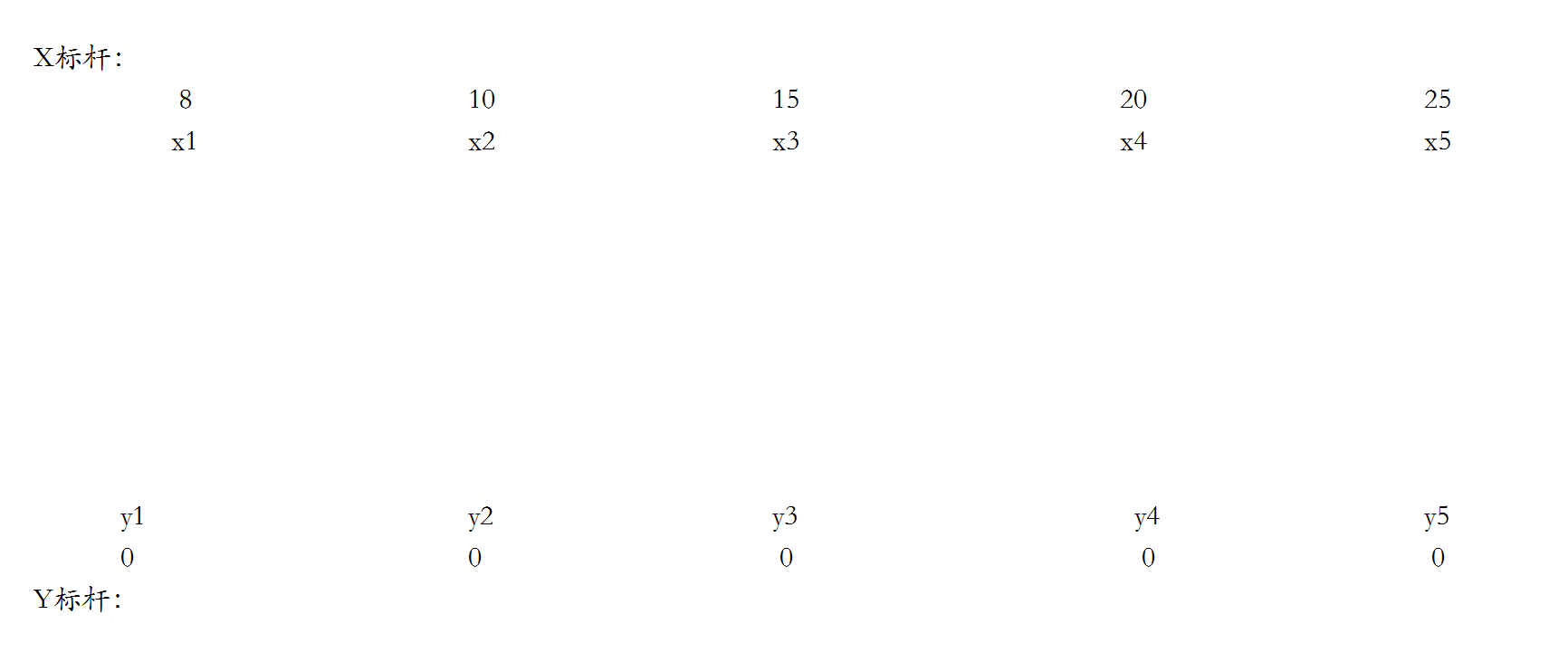

连接每条边并且使得x1和y3匹配，然后遍历x2，发现x2找不到合法增广路。

把不合法路径上的x点都归为点集S,y点都归为T,将不在T中的y点和在S中的点尝试进行加边。

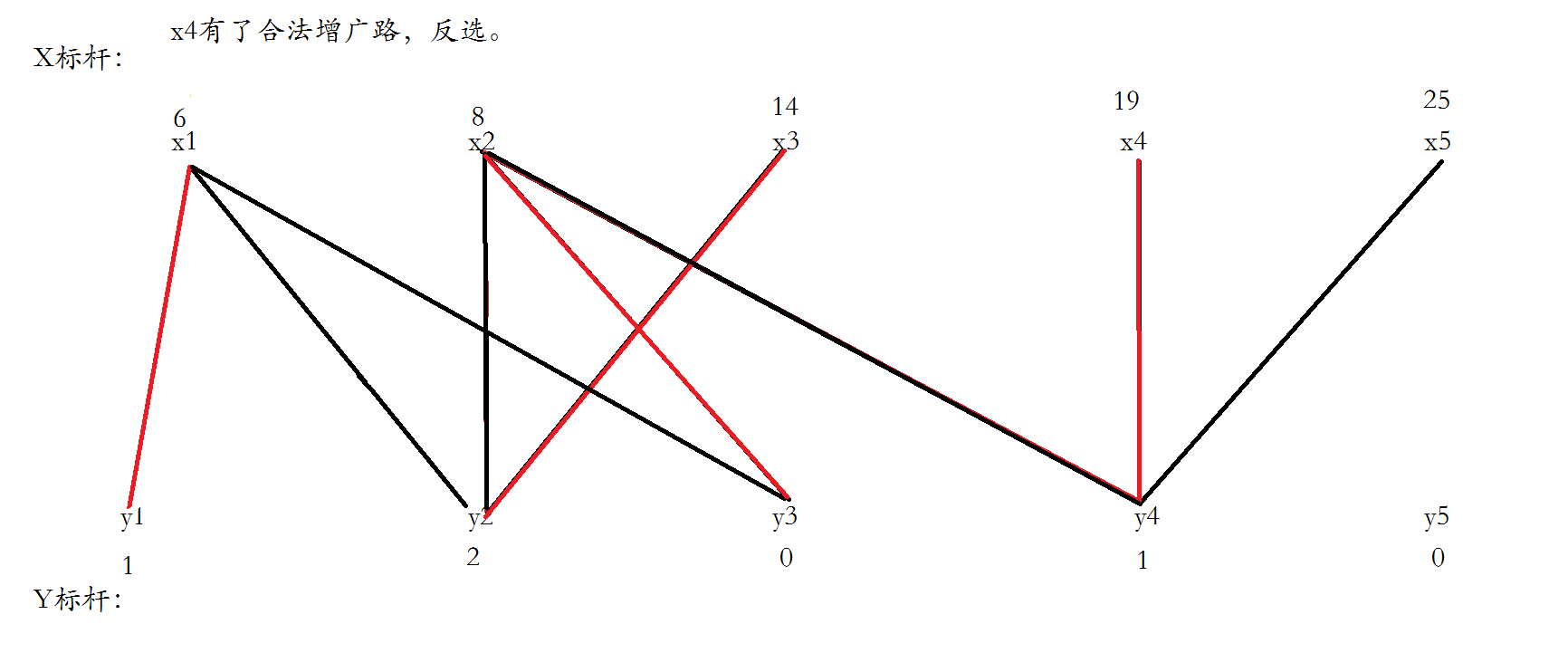
找到两条边，更新顶标之后，成功形成增广路，运用匈牙利算法反选。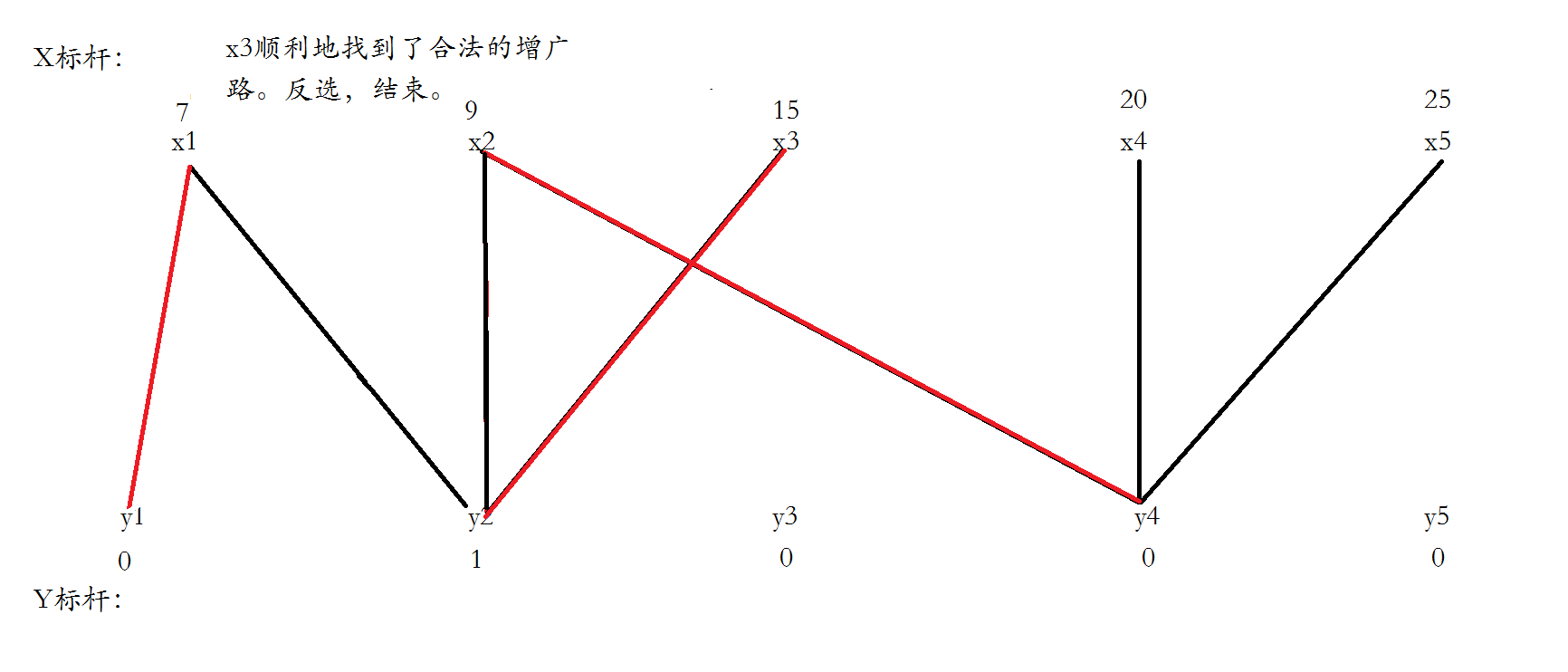

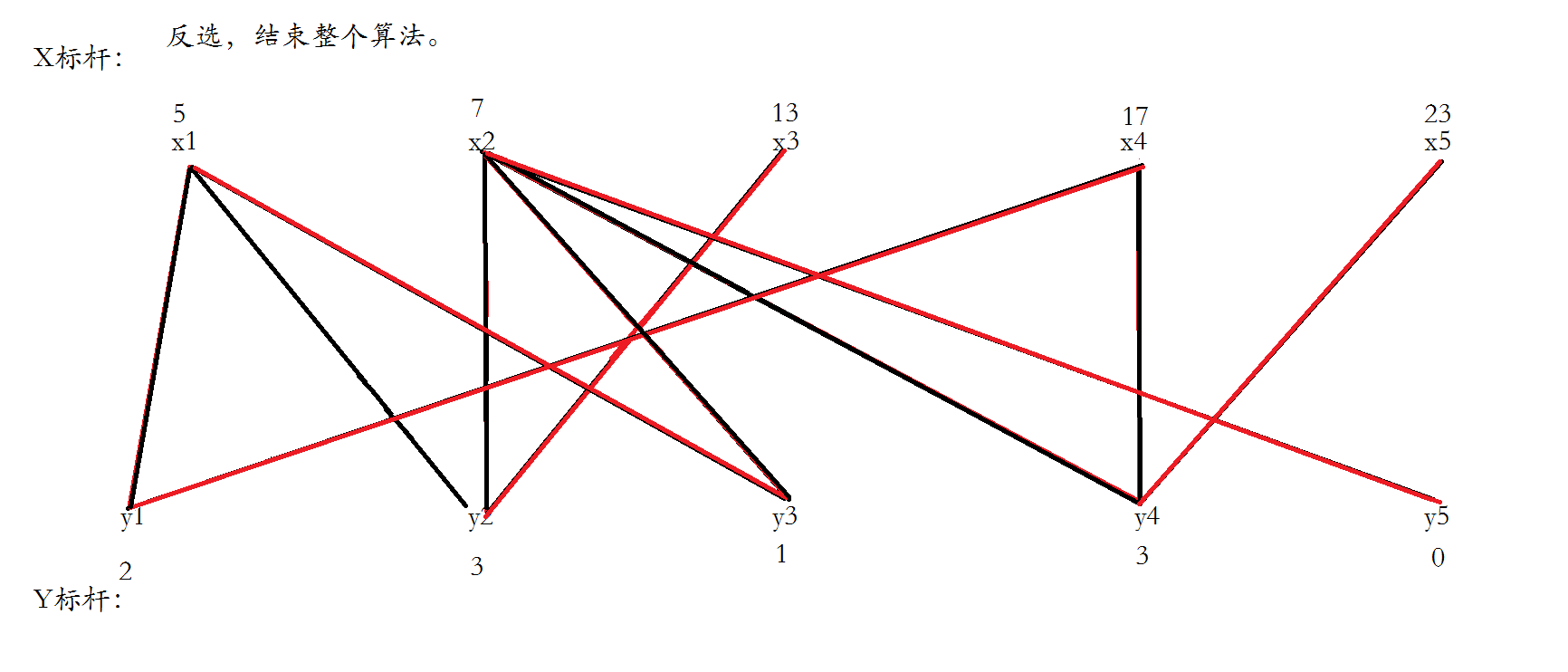
给x3找一个合法的增广路，一下就找到了，直接反选，结束。

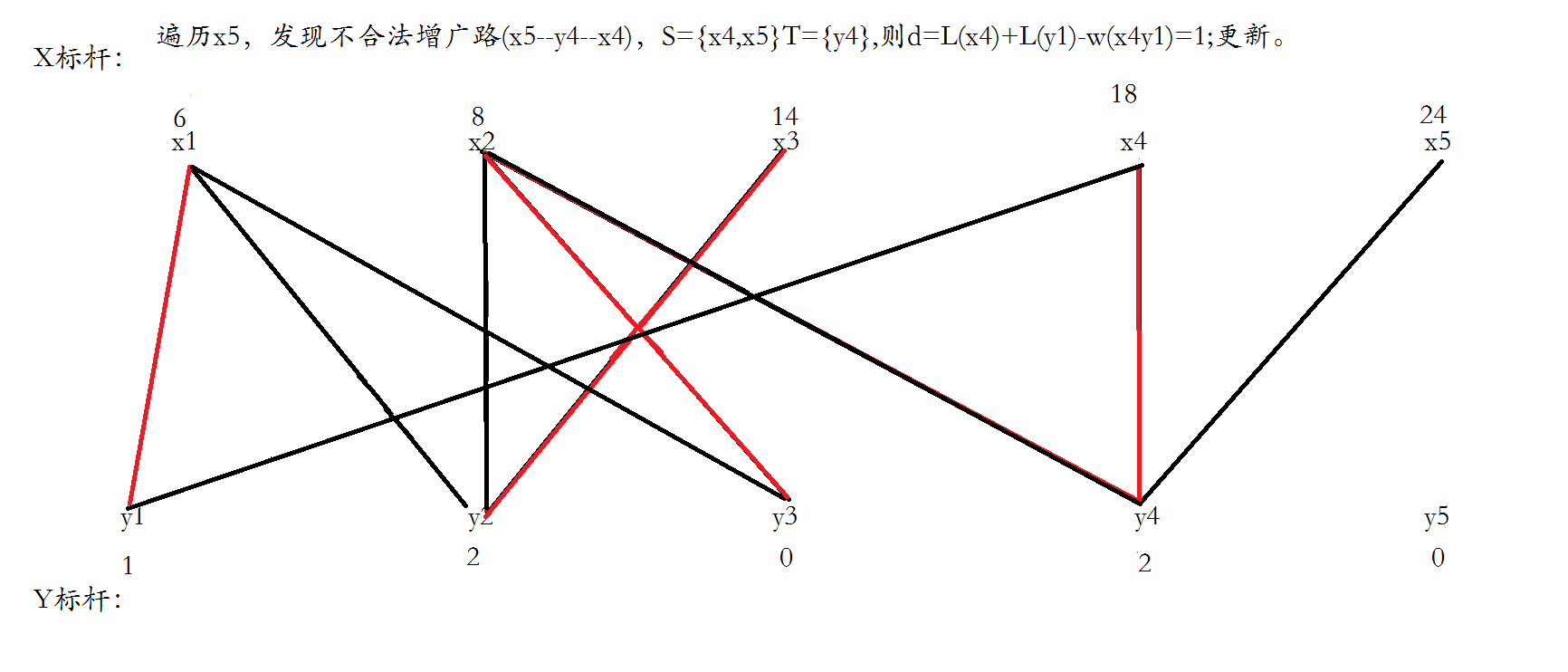
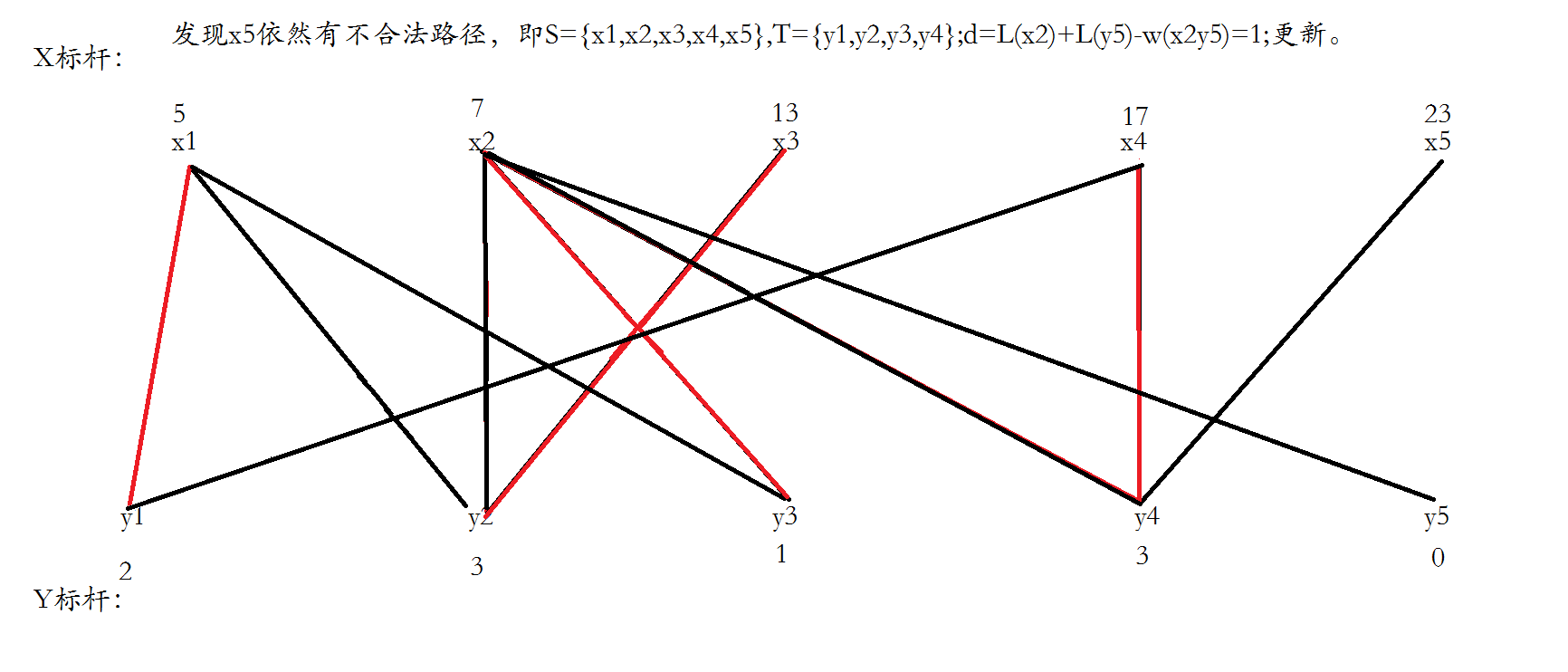
下面不对，应该只有一条不合法路径，S={x2,x3,x4},T={y2,y4}，所以x1和y1不变。

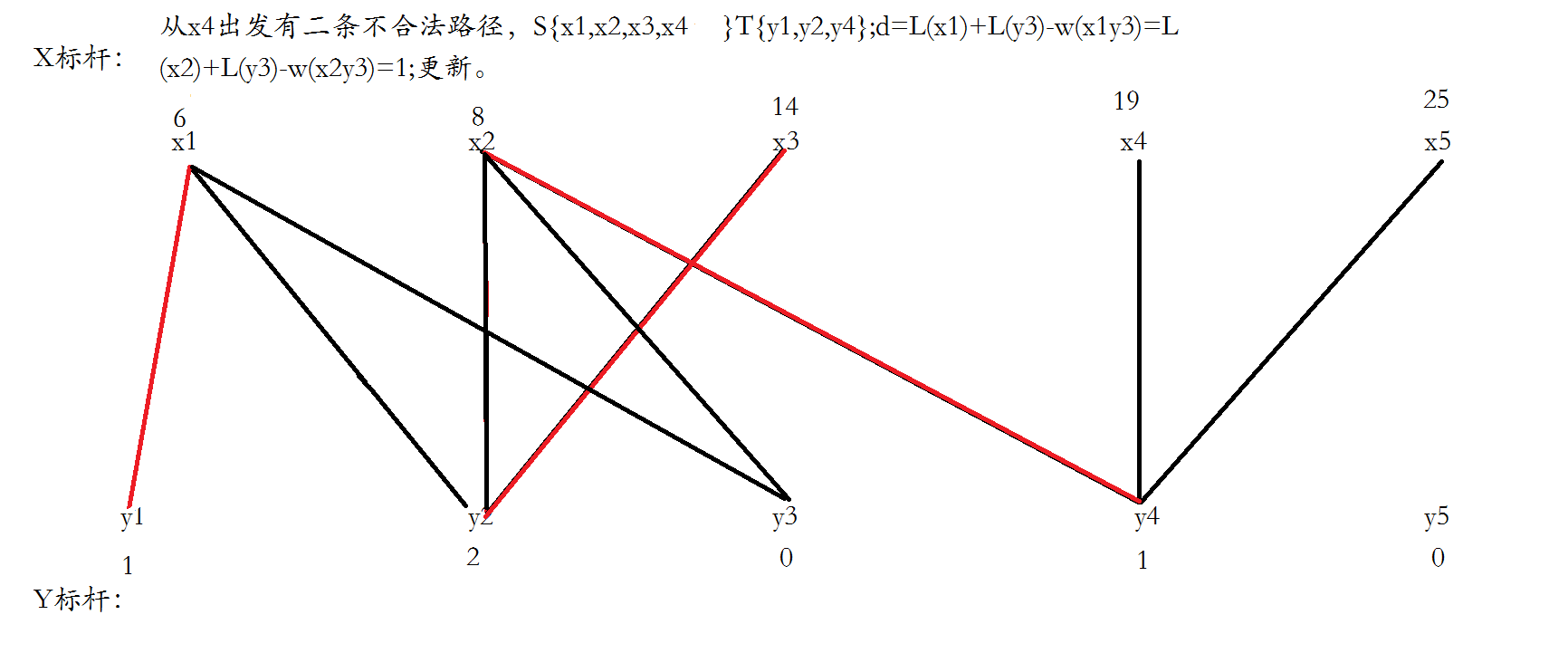
一个优化是对Y顶点引入松弛函数slack，slack[j]保存跟当前节点j相连的节点i的lx[i]+ly[j]−weight(i,j)的最小值，于是求delta时只需O(n)枚举不在交错树中的Y顶点的最小slack值即可。

松弛值可以在匈牙利算法检查相等子树边失败时进行更新，同时在修改标号后也要更新，具体参考代码实现。

如果我们要求边权值最小的匹配呢？？？

我们可以把边权值取负值，得出结果后再取相反数就可以了。

以HDU 2255为例

const int INF = 0x3f3f3f3f;
using namespace std;
int nx,ny;
int w[310][310];
int lx[310],ly[310];
int link[310];//右边对应的左边的编号
bool visx[310],visy[310];
int slack[310];//跟当前节点j相连的节点i的lx[i]+ly[j]−weight(i,j)的最小值
bool dfs(int id)//寻找增广路
{
    visx[id]=true;
    for(int i=0;i<ny;i++)
    {
        if(visy[i])continue;
        int temp=lx[id]+ly[i]-w[id][i];
        if(temp==0)//“lx[t]+ly[i]==w[t][i]”决定了这是在相等子图中找增广路的前提
        {
            visy[i]=true;
            if(link[i]==-1||dfs(link[i]))
            {
                link[i]=id;
                return true;
            }
        }
        else slack[i]=min(slack[i],temp);//(x,y)不在相等子图中且y不在交错树中
    }
    return false;
}
int KM()
{
    memset(link,-1,sizeof(link));
    memset(ly,0,sizeof(ly));
    for(int i=0;i<nx;i++)
    {
        lx[i]=-INF;
        for(int j=0;j<ny;j++)
            lx[i]=max(lx[i],w[i][j]);
    }
    for(int i=0;i<nx;i++)
    {
        for(int j=0;j<ny;j++)slack[j]=INF;//每次换新的x结点都要初始化slack
        while(1)//如果没有找到一条合法增广路，就一直加边
        {
            memset(visx,0,sizeof(visx));
            memset(visy,0,sizeof(visy));
            if(dfs(i))break;//找到增广路，退出
            int d=INF;//否则，应该加入新的边，计算d的值
            for(int j=0;j<ny;j++)
                if(!visy[j])d=min(d,slack[j]);
            //if(d==INF)return -1;//找不到可以加入的边，即没有完美匹配
            for(int j=0;j<nx;j++)
                if(visx[j])lx[j]-=d;
            for(int j=0;j<ny;j++)
            {
                if(visy[j])ly[j]+=d;
                else slack[j]-=d;
                //修改顶标后，要把所有的slack值都减去delta
                //这是因为lx[i] 减小了delta
                //slack[j] = min(lx[i] + ly[j] -w[i][j]) --j不属于交错树--也需要减少delta
            }
        }
    }
    int sum=0;
    for(int i=0;i<ny;i++)
    {
        if(link[i]!=-1)
            sum+=w[link[i]][i];
    }
    return sum;
}
int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        nx=ny=n;
        //memset(w,0,sizeof(w));
        for(int i=0;i<nx;i++)
            for(int j=0;j<ny;j++)
                scanf("%d",&w[i][j]);
        printf("%d\n",KM());
    }
    return 0;
}

二分图多重匹配

二分图多重最大匹配：

在原图上建立源点S和汇点T，S向每个X方点连一条容量为该X方点L值的边，每个Y方点向T连一条容量为该Y方点L值的边，原来二分图中各边在新的网络中仍存在，容量为1（若该边可以使用多次则容量大于1），求该网络的最大流，就是该二分图多重最大匹配的值。

二分图多重最优匹配：
在原图上建立源点S和汇点T，S向每个X方点连一条容量为该X方点L值、费用为0的边，每个Y方点向T连一条容量为该Y方点L值、费用为0的边，原来二分图中各边在新的网络中仍存在，容量为1（若该边可以使用多次则容量大于1），费用为该边的权值。求该网络的最大费用最大流，就是该二分图多重最优匹配的值。

以hihocoder1393为例：https://hihocoder.com/problemset/problem/1393

题意：

班级一共有N名学生，编号依次为1..N。运动会一共有M项不同的比赛，编号为1..M。第i项比赛每个班需要派出m[i]名选手参加。

编号为i的学生表示最多同时参加a[i]项比赛，并且给出他所擅长的b[i]项比赛的编号。

要求将每个学生都安排到他所擅长的比赛项目，以增加夺冠的可能性。同时又要考虑满足每项比赛对人数的要求，当然给一个学生安排的比赛项目也不能超过他愿意参加的比赛项目数量。

问能否有一个合适的安排，同时满足这些条件。

思路：

将学生看作A部，比赛项目看作B部，比如编号为i的学生擅长编号为j的项目，那么就连接A[i]-B[j]。

因为A[i]最多只能和a[i]的点相连。所以我们需要一个方法来限制这个量在0~a[i]之间变动，有点像网络流里面的流量，只能在0和容量之间变动。

首先虚拟一个源点s和汇点t，在s和A[i]之间连接一条容量为a[i]的边，将原来A[i]-B[j]直接的边都改造为从A[i]到B[j]的容量为1的边，由于比赛项目B[j]最多只需要m[j]名选手参加，所以我们不妨限制B[j]-t的容量为m[j]。

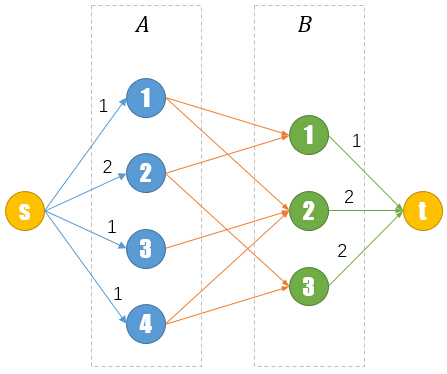
s-A[i]：这一类边的流量表示了A[i]参加的项目数量。

A[i]-B[j]：这一类边的流量表示了A[i]是否参加项目B[j]，若参加则流量为1，否则流量为0。

B[j]-t：这一类边的流量表示了参加比赛项目B[j]的选手数量。

由于流网络会自动调整去满足最大流量，所以它会自动调整每个A[i]-B[j]的流量来使得B[j]-t尽可能大。

若每个项目都能够满足人数的话，网络流会自己调整为所有B[j]-t都满流的情况。

只需要最后判断一下每一条B[j]-t的边是否满流，就可以知道能否满足需求。同时还可以根据A[i]-B[j]的情况，计算出每个选手所参加的比赛项目。

代码：

const long long INF=0x3f3f3f3f3f3f3f3f;
int n,m;
int s,e;//源点、汇点
int top;
struct edge
{
    int to;
    long long cap;
    int next;
}eg[100010];//邻接表要开边数的两倍
int head[210];
int cur[210];
int dis[210];
void add(int x,int y,long long z)
{
    eg[top].cap=z;
    eg[top].to=y;
    eg[top].next=head[x];
    head[x]=top++;
}
bool bfs()
{
    memset(dis,-1,sizeof(dis));
    queue<int>q;
    dis[s]=0;
    q.push(s);
    while(!q.empty())
    {
        int id=q.front();
        q.pop();
        for(int i=head[id];i!=-1;i=eg[i].next)
        {
            int temp=eg[i].to;
            if(dis[temp]==-1&&eg[i].cap>0)
            {
                dis[temp]=dis[id]+1;
                q.push(temp);
                if(temp==e)break;
            }
        }
    }
    return dis[e]!=-1;
}
long long dfs(int id,long long cp)
{
    if(id==e||cp==0)return cp;
    long long res=0,f;
    for(int i=cur[id];i!=-1;i=eg[i].next)
    {
        int temp=eg[i].to;
        if(dis[temp]==dis[id]+1)
        {
            f=dfs(temp,min(cp-res,eg[i].cap));
            if(f>0)
            {
                eg[i].cap-=f;
                eg[i^1].cap+=f;
                res+=f;
                if(res==cp)return cp;
            }
        }
    }
    if(res==0)dis[id]=-1;
    return res;
}
long long dinic()
{
    long long ans=0;
    while(bfs())
    {
        for(int i=0;i<=n+m+1;i++)
            cur[i]=head[i];
        ans+=dfs(s,INF);
    }
    return ans;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        long long x;
        int y;
        int z;
        scanf("%d%d",&n,&m);//学生/比赛
        top=0;
        memset(head,-1,sizeof(head));
        s=0;e=n+m+1;
        long long sum=0;
        for(int i=1;i<=m;i++)
        {
            scanf("%lld",&x);
            sum+=x;
            add(n+i,e,x);
            add(e,n+i,0);
        }
        for(int i=1;i<=n;i++)
        {
            scanf("%lld",&x);
            add(s,i,x);
            add(i,s,0);
            scanf("%d",&y);
            while(y--)
            {
                scanf("%d",&z);
                z+=n;
                add(i,z,1);
                add(z,i,0);
            }
        }
        if(dinic()==sum)printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

最小路径覆盖的网络流做法

hihocoder1394：http://hihocoder.com/problemset/problem/1394

代码：

const long long INF=0x3f3f3f3f3f3f3f3f;
int n;
int s,e;//源点、汇点
int top;
struct edge
{
    int to;
    long long cap;
    int next;
}eg[100010];//邻接表要开边数的两倍
int head[1010];
int cur[1010];
int dis[1010];
void add(int x,int y,long long z)
{
    eg[top].cap=z;
    eg[top].to=y;
    eg[top].next=head[x];
    head[x]=top++;
}
bool bfs()
{
    memset(dis,-1,sizeof(dis));
    queue<int>q;
    dis[s]=0;
    q.push(s);
    while(!q.empty())
    {
        int id=q.front();
        q.pop();
        for(int i=head[id];i!=-1;i=eg[i].next)
        {
            int temp=eg[i].to;
            if(dis[temp]==-1&&eg[i].cap>0)
            {
                dis[temp]=dis[id]+1;
                q.push(temp);
                if(temp==e)break;
            }
        }
    }
    return dis[e]!=-1;
}
long long dfs(int id,long long cp)
{
    if(id==e||cp==0)return cp;
    long long res=0,f;
    for(int i=cur[id];i!=-1;i=eg[i].next)
    {
        int temp=eg[i].to;
        if(dis[temp]==dis[id]+1)
        {
            f=dfs(temp,min(cp-res,eg[i].cap));
            if(f>0)
            {
                eg[i].cap-=f;
                eg[i^1].cap+=f;
                res+=f;
                if(res==cp)return cp;
            }
        }
    }
    if(res==0)dis[id]=-1;
    return res;
}
long long dinic()
{
    long long ans=0;
    while(bfs())
    {
        for(int i=0;i<=2*n+1;i++)
            cur[i]=head[i];
        ans+=dfs(s,INF);
    }
    return ans;
}
int main()
{
    int m,x,y;
    scanf("%d%d",&n,&m);
    top=0;
    memset(head,-1,sizeof(head));
    s=0;e=2*n+1;
    for(int i=1;i<=n;i++)
        add(s,i,1),add(i,s,0);
    for(int i=n+1;i<=2*n;i++)
        add(i,e,1),add(e,i,0);
    while(m--)
    {
        scanf("%d%d",&x,&y);
        add(x,n+y,1),add(n+y,x,0);
    }
    printf("%lld\n",n-dinic());
    return 0;
}

二分图常用建图方法

行列匹配法

上图是一个 3 * 3 的矩阵，方格内的 1 表示这个地方有敌人，0 表示没有敌人,现在我们有很多箭，每根箭可以杀死一行或者一列的敌人，问我们要杀死所有的敌人至要用到几根箭？
我们要杀死某个敌人，只要让他所在的行列有箭经过就行。也就是所有的位置都被箭覆盖就行，就是顶点的最小覆盖，既然是顶点的最小覆盖，而且我们要杀的是敌人，那么我们的点就应该是敌人的位子，即(行列)对于上面那个图我么可以建立下面这个模型：

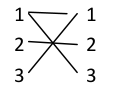
一个二分图的最小顶点覆盖就是要找到最少的边把所有的顶点覆盖，二分图的最小顶点覆盖是等于二分图的最大匹配。所以我们只需要对上面的那个二分图就最大匹配就行。

黑白染色法

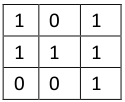
又是一个图，要求是把方格里的所有的 1 改为零，一次最多只能修改相邻的两个，问最少需要修改几次?

既然是每次只能拿相邻的两个，正好我们匹配的时候也是找两个进行匹配，这是否就是这个题和最大二分图匹配相联系的地方呢？但是每个点能和他四周的四个点匹配,那么我们怎么把所有的点分成两个部分呢？就是要把第i个点放到第一部分，第i个点周围的四个点放到第二部分，再把这四个点周围的点放到第一部分。有了这样的思想，我们只需对原图做这样的改动：黑白染色使四周和中间的颜色不同。

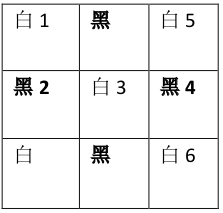
图中黑白的意思是就是把点分类，图里的 1,2,3,4,5,6 表示的就是上面那个 0，1 图的1 的个数，然后建图，把相邻的点相连，比如说1和2，2和3。

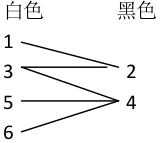
然后要把所有一改为零，也就是要对每个点都操作，每个点都要有，那不就是最小顶点覆盖吗？这个问题解决了。

反建法

问题背景:一个极度封建的老师要带同学们出去玩,但是他怕在途中同学之间发生恋情老师研究了一下发现,满足下面几种条件的两个同学之间发生恋情的可能性很小
1）身高差 > 40
2）性别相同
3）爱好不同的音乐
4）爱好同类型的运动
显然如果我们用满足上面条件的同学之间建边那么最后建立起来的就不是二分图了。稍微观察一下,男生之间我们是随便带的,女生也是,因为他们彼此性别相同。因此我们就可以把男女分为两部分,那么男女之间如何建边?如果我们把男女满足不发生恋情的连起来,那么求出来的最大匹配没有代表性,不能得到我们想要的结果。因此我们用反建法,把男女中可能发生恋情的建立边。也就是说把身高差<=40 或 爱好相同音乐或爱好不同类型运动的男女同学之间用边连起来。然后求一个最大独立集,最大独立集的原则不就是找到一个点集,使得集合内的点互不相连且点尽量多吗?我们把可能发生恋情的男女相连,那么最大独立集不就是我们要找的不可能发生恋情的人的集合吗? 那么, 这个问题解决了!

拆点法

拆点法是用于解决最小路径覆盖问题的,给出一个图

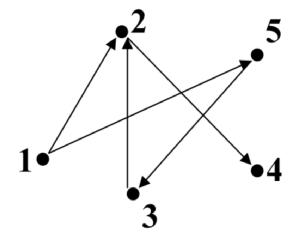
要找到几条路径,可以把所有的点经过,并且路径之间不可以交叉。我们的做法是把点拆成两部分(点 1 拆为 x1,y1. 点 2 拆为 x2,y2……)

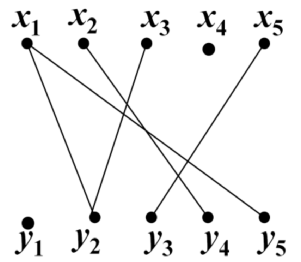
如果我们对这个图求二分图的最大匹配,你会发现每个匹配对应着一个路径覆盖,因此,此二分图的最大匹配即:原图中的最小路径覆盖上的边的个数(路径是由 0 条,1 条或多条边组成的)。那么原图的最小路径覆盖数 = 原图顶点数 – 最小路径上的边数 也就是 原图的最小路径覆盖数 = 原图顶点数 – 二分图最大匹配数。

一行变多行,一列变多列

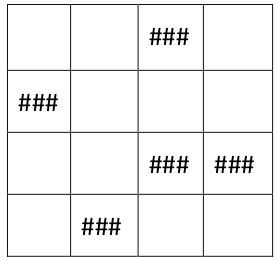
上面是一个 4*4 的方格,方格内的###表示墙,我们要在表格内没有墙的地方建立碉堡,而且要保证任何两个碉堡之间互相不能攻击,问最多能建多少个碉堡?是否感觉像第一个题呢?如果我们向第一个题那样建图,那么最后求出来的最大匹配也就是行和列的匹配。而且这个匹配满足了所有匹配都是不同行不同列(匹配本身的性质就是每个点至多属于匹配中的某个边)。但是这样的建图的话,我们墙怎么处理? 有墙的地方就相当于把这一行和这一列分成了两行,两列。
例如

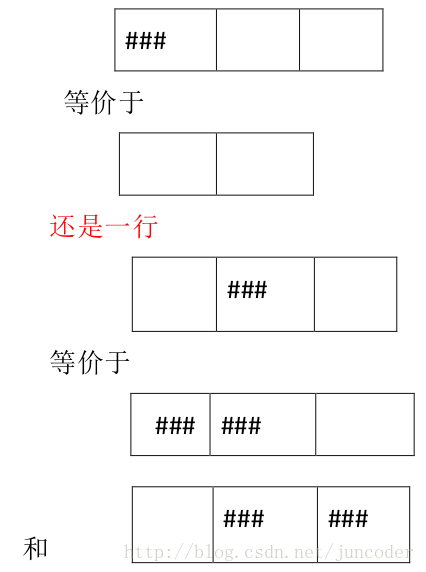
一行变成了两行。

然后我们按照这个编号建图即可

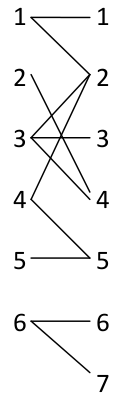
对这个图求二分图最大匹配即可。这个问题也解决了!