网络流 - Blog

最大流及Dinic算法

网络流的最大流算法就是指的一个流量的方案使得网络中流量最大。

网络流最大流的求解：

网络流的所有算法都是基于一种增广路的思想，下面首先简要的说一下增广路思想，其基本步骤如下：

1.找到一条从源点到汇点的路径，使得路径上任意一条边的残量>0（注意是小于而不是小于等于，这意味着这条边还可以分配流量），这条路径便称为增广路
2.找到这条路径上最小的F(u)(v)（我们设F(u)(v)表示u->v这条边上的残量即剩余流量），下面记为flow
3.将这条路径上的每一条有向边u->v的残量减去flow，同时对于起反向边v->u的残量加上flow（为什么呢？我们下面再讲）
4.重复上述过程，直到找不出增广路，此时我们就找到了最大流

这个算法是基于增广路定理(Augmenting Path Theorem): 网络达到最大流当且仅当残留网络中没有增广路。

Dinic 算法：
基本思路:

1.根据残量网络计算层次图。
2.在层次图中使用DFS进行增广直到不存在增广路。
3.重复以上步骤直到无法增广。

较详细解释(流程) :

1.用BFS建立分层图注意:分层图是以当前图为基础建立的,所以要重复建立分层图。
2.用DFS的方法寻找一条由源点到汇点的路径,获得这条路径的流量I 根据这条路径修改整个图,将所经之处正向边流量减少I,反向边流量增加I,注意I是非负数。
3.重复步骤2,直到DFS找不到新的路径时,重复步骤1。

当前弧优化：

对于每个点，我可能在一次BFS之后DFS多次。那么它出发的边所到的点里，有些点出发已经满流。

这样，我就可以每个点记录一个当前弧，表示这次DFS它最后DFS到哪条弧，下次DFS它的时候就从这条弧开始。

这样，我就可以保证每条边在一次DFS中满流后不会再遍历。

模板：

typedef long long ll;
const long long INF=0x3f3f3f3f3f3f3f3f;
int n;
int s,e;//源点、汇点
int top;
struct edge
{
    int to;
    ll cap;
    int next;
}eg[200010];//邻接表要开边数的两倍
int head[10010];
int cur[10010];//当前弧优化
int dis[10010];//分层图中每个点的层数（即到原点的最短距离）
void add(int x,int y,ll z)
{
    eg[top].cap=z;
    eg[top].to=y;
    eg[top].next=head[x];
    head[x]=top++;
}
bool bfs()
{
    memset(dis,-1,sizeof(dis));
    queue<int>q;
    dis[s]=0;
    q.push(s);
    while(!q.empty())
    {
        int id=q.front();
        q.pop();
        for(int i=head[id];i!=-1;i=eg[i].next)
        {
            int temp=eg[i].to;
            if(dis[temp]==-1&&eg[i].cap>0)
            {
                dis[temp]=dis[id]+1;
                q.push(temp);
                if(temp==e)break;
            }
        }
    }
    return dis[e]!=-1;//能否到汇点，不能就结束
}
ll dfs(int id,ll cp)//id为当前节点，cp为当前最小残量
{
    if(id==e||cp==0)return cp;//流到终点了或者没有流了
    ll res=0,f;//ret:本次搜索能找到的所有流量，f：本次搜索一条路径的可以通过的流量
    for(int i=cur[id];i!=-1;i=eg[i].next)
    {
        int temp=eg[i].to;
        if(dis[temp]==dis[id]+1)
        {
            f=dfs(temp,min(cp-res,eg[i].cap));//能通的流就等于搜过后面之后允许的流，和自己允许的流的最小值
            if(f>0)
            {
                eg[i].cap-=f;
                eg[i^1].cap+=f;//反向边剩余流量加上f
                res+=f;
                if(res==cp)return cp;
            }
        }
    }
    if(res==0)dis[id]=-1;
    return res;
}
ll dinic()
{
    ll ans=0;
    while(bfs())//建立分层图
    {
        for(int i=1;i<=n;i++)
            cur[i]=head[i];//每一次建立完分层图后都要把cur置为每一个点的第一条边//？？？
        ans+=dfs(s,INF);//只要有路就走,假设它有无限流，再慢慢调整
    }
    return ans;
}
int main()
{
    int m;
    while(scanf("%d%d%d%d",&n,&m,&s,&e)!=EOF)
    {
        top=0;
        memset(head,-1,sizeof(head));
        while(m--)
        {
            int x,y;
            ll z;
            scanf("%d%d%lld",&x,&y,&z);
            add(x,y,z);
            add(y,x,0);
        }
        printf("%lld\n",dinic());
    }
    return 0;
}

最大流最小割定理

在一个有权图中，源点为Vs，汇点为Vt，如果拿掉这张图中的一些边，就无法从Vs到达Vt，这些边的组合就叫做割集。

对于一个网络流图G=(V,E)，其割的定义为一种点的划分方式：将所有的点划分为S和T=V-S两个部分，其中源点s∈S，汇点t∈T。

对于一个割(S,T)，我们定义净流f(S,T)表示穿过割(S,T)的流量之和，即：

f(S,T) = Σf(u,v) | u∈S,v∈T
举个例子：

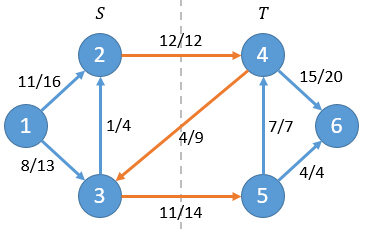
净流f = f(2,4)+f(3,4)+f(3,5) = 12+(-4)+11 = 19

同时我们定义割的容量C(S,T)为所有从S到T的边容量之和，即：

C(S,T) = Σc(u,v) | u∈S,v∈T

割的容量：所有正向割边的容量和

同样在上面的例子中，其割的容量为：

c(2,4)+c(3,5)=12+14=26

实际上对于任意一个割的净流f(S,T)总是和网络流的流量f相等。比如上面例子中我们改变一下割的方式：

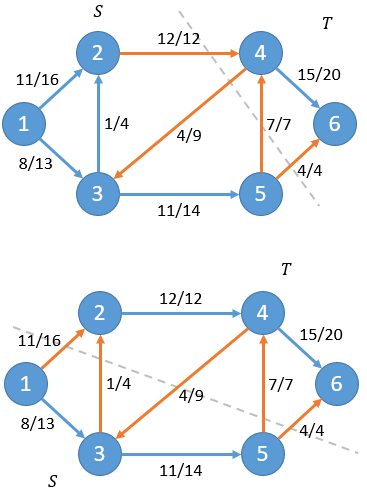
可以计算出对于这两种情况净流f(S,T)仍然等于19。

任意一个割的净流f(S,T)都等于当前网络的流量f。

对于网络的任意一个流f一定是小于等于任意一个割的容量C(S,T)。

而在所有可能的割中，存在一个容量最小的割，我们称其为最小割。

对于任一个网络流图来说，其最大流一定是小于等于最小割的。

最大流最小割定理：

对于一个网络流图G=(V,E)，其中有源点s和汇点t，那么下面三个条件是等价的：

流f是图G的最大流

残留网络Gf不存在增广路

对于G的某一个割(S,T)，此时f = C(S,T)

首先有割的容量C(S,T)=T中所有正权点的权值之和+S中所有负权点的权值绝对值之和。

最小费用最大流

费用流建立在网络最大流的基础上，一张图中最大流有且仅有一个，但是最大流条数往往不止一条，这时候对于我们来说，可能要找出这些最大流中最小（或者最大）的那一条路径（贪心策略嘛），这就是最小（最大）费用最大流

typedef long long ll;
const ll INF=0x3f3f3f3f3f3f3f3f;
int n;
int s,e;//源点、汇点
ll ans;//最大流量情况下的最小费用
int top;
struct edge
{
    int to;
    ll cap;
    ll cost;
    int next;
}eg[100010];//邻接表要开边数的两倍
int head[5010];
bool vis[5010];
ll dis[5010];
void add(int a,int b,ll c,ll d)
{
    eg[top].cap=c;
    eg[top].cost=d;
    eg[top].to=b;
    eg[top].next=head[a];
    head[a]=top++;
}
bool spfa(int ss,int ee)
{
    memset(vis,0,sizeof(vis));
    for(int i=0;i<=n;i++)
        dis[i]=INF;
    dis[ee]=0;vis[ee]=true;
    deque<int>q;
    q.push_back(ee);
    while(!q.empty())
    {
        int temp=q.front();
        q.pop_front();
        for(int i=head[temp];i!=-1;i=eg[i].next)
        {
            int tp=eg[i].to;
            if(eg[i^1].cap&&dis[tp]>dis[temp]-eg[i].cost)
            {
                dis[tp]=dis[temp]-eg[i].cost;
                if(!vis[tp])
                {
                    vis[tp]=true;
                    if(!q.empty()&&dis[tp]<dis[q.front()])q.push_front(tp);
                    else q.push_back(tp);
                }
            }
        }
        vis[temp]=false;
    }
    return dis[ss]<INF;
}
ll dfs(int x,ll cp)
{
    if(x==e)
    {
        vis[e]=true;
        return cp;
    }
    ll used=0,a;
    vis[x]=true;
    for(int i=head[x];i!=-1;i=eg[i].next)
    {
        int temp=eg[i].to;
        if(!vis[temp]&&eg[i].cap&&dis[x]-eg[i].cost==dis[temp])
        {
            a=dfs(temp,min(eg[i].cap,cp-used));
            if(a)
            {
                ans+=a*eg[i].cost;
                eg[i].cap-=a;
                eg[i^1].cap+=a;
                used+=a;
            }
            if(used==cp)break;
        }
    }
    return used;
}
ll costflow()
{
    ll flow=0;
    while(spfa(s,e))
    {
        vis[e]=1;
        while(vis[e])
        {
            memset(vis,0,sizeof(vis));
            flow+=dfs(s,INF);
        }
    }
    return flow;
}
int main()
{
    int m;
    while(scanf("%d%d%d%d",&n,&m,&s,&e)!=EOF)
    {
        top=0;
        memset(head,-1,sizeof(head));
        while(m--)
        {
            int a,b;
            ll c,d;
            scanf("%d%d%lld%lld",&a,&b,&c,&d);
            add(a,b,c,d);
            add(b,a,0,-d);
        }
        ans=0;
        ll temp=costflow();//最大流
        printf("%lld %lld\n",temp,ans);
    }
    return 0;
}